Account tree
Contents
The account tree is 1 of the 3 core components of the mini-blockchain scheme. Why should we record every single transaction and save it forever if all we need to know is the balance of all non-empty addresses? The 2nd function of the blockchain is replaced with the account tree. The account tree is essentially what could be thought of as a decentralized "balance sheet". Each account in the account tree will hold the address and the balance of that address, along with a few other fields related to withdrawal limits.
When the balance of an address changes all we need to do is update numbers in the account tree instead of adding new data to it. Of course this wont provide a truly finite amount of data to work with because new non-empty addresses will be appearing all the time, but it comes as close to finite as is probably possible. It is finite in some sense because the coins will have limited divisibility, and we can't really expect the world population or the number of Internet users to continue growing forever. In any case it's scalable and manageable.
Even with a population of 10 billion people where each person had 10 different non-empty addresses, we would only need to keep track of 100 billion addresses. Since we can remove empty addresses from the database and since a transaction would simply require peers to shift around numbers in this database instead of adding new data to it, the size of the account tree should always remain considerably small. By the time we reach anything close to 100 billion unique non-empty addresses our computers will be much faster.
Owners of a non-empty address in the account tree would prove their ownership with their private key. Like Bitcoin, transactions are created as a signed set of data and broadcast over the network. Like Bitcoin, miners who accept the transaction then put it into their blocks and work on solving a difficult problem to get it into the mini-blockchain (see proof chain page). Nodes who accept the block would update their own copy of the account tree by shifting around coins or doing what ever was necessary.
The proposed database is named the “account tree” because it should have a hash tree structure. Each account in the tree has a corresponding hash and acts as a leaf node at the bottom of the tree. Being a hash tree, we can combine the hashes of each account to build a pyramid of hashes and calculate the master hash at the top. Note that an “account” isn't a collection of addresses like a “Bitcoin account”. In this case each account refers to only one address or leaf node (obviously normal “accounts” will also exist).
Requirements of Account Tree Structure
There are a number of ways the account tree can be implemented, but the data structure must fulfill certain requirements.
- All data should be able to be efficiently compacted to a deterministic hash (master hash / ledger fingerprint).
- Efficient support for 4 operations: add account, modify account, remove account, lookup account.
- After every modification one should be able to efficiently update the account tree master hash.
- Should allow referencing of accounts by offset and address.
- Should allow one to efficiently verify the correctness of a subset of the accounts without downloading the entire ledger.
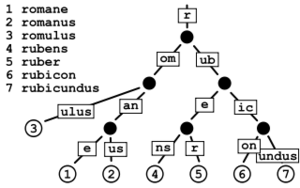
Binary Radix Trie
Figure 0-a shows a generic radix trie structure (from Wikipedia). In reality Cryptonite uses a type of binary radix trie combined with merkle hashing. What isn't shown in the diagram is how the nodes are hashed. All the hashes together produce the master hash/root hash at the top. The master hash will change even if just one account within the tree is altered in any way. This hash tree system provides integrity to our data because the master hash is also stored in block headers so the tree is secured by the blockchain.
The advantages of using a binary radix trie structure include:
- it is well suited for looking up addresses (public key hashes)
- it is faster and more memory efficient than many other tree structures
- small parts of the tree can be verified without the whole and completeness can be proven
- inserting the same data into the trie in any order will always generate the same structure
New accounts are inserted into the trie structure as leaf nodes when coins are sent to an address which does not already exist and they are removed from the trie when the address is emptied. When the address does exist the transaction will simply alter an existing account in the trie. The mini-blockchain acts to coordinate when the tree is updated. When a node receives a new block they will carry out the transactions listed within the block by altering their account tree accordingly.
Interaction with Mini-Blockchain
The proposed account tree structure allows all address balances to be summarized in a "balance sheet" format and allows old transactions to be safely discarded by all nodes. However, without a way to coordinate when and how the account tree is changed we still can't ensure consistency between nodes. That is where the mini-blockchain comes in. Each time a new block is accepted into the mini-blockchain, nodes will use that block to update their copy of the account tree in a consistent and coordinated fashion.
In a distributed network it is impossible for every node to apply transactions at the moment it sees them. Transactions must be joined together and applied in bulk. Such a list of transactions grouped together form a block and together with headers form the blockchain. Nodes collect the transactions and apply them to the account tree to achieve a new account tree state. The master hash of the new tree state is included in the block header. Other nodes which receive such blocks can replay transactions themselves and check the hashes match.
Defining Allowed Modifications of Account Tree
The account tree structure defined here can be used for almost any model of underlying data. Rules which define how the tree can be modified define how it really works. Single operations on the ledger are called transactions. The types of allowed transactions will define how the currency actually functions.